Logarit là một khái niệm quan trọng trong toán học, đặc biệt là trong lĩnh vực đại số và giải tích. Việc nắm vững các công thức logarit không chỉ giúp bạn giải quyết các bài toán phức tạp mà còn mở ra nhiều ứng dụng thực tiễn trong khoa học và kỹ thuật. Bài viết này sẽ cung cấp một cái nhìn tổng quan về các công thức logarit, tính chất của chúng và cách áp dụng vào thực tế. Ngoài ra, chúng ta cũng sẽ nhắc đến trang web giasutoanvan.com như một nguồn tài liệu hữu ích cho việc học tập và tra cứu.

1. Khái Niệm Về Logarit
Logarit là phép toán ngược của lũy thừa. Nếu (a^x = b), thì logarit cơ số (a) của (b) được ký hiệu là (\log_a b) và được định nghĩa là (x). Nói cách khác, (\log_a b = x) nếu (a^x = b).
Ví dụ:
- (\log_{10} 100 = 2) vì (10^2 = 100)
- (\log_2 8 = 3) vì (2^3 = 8)
2. Các Công Thức Logarit Cơ Bản
Dưới đây là một số công thức logarit cơ bản mà bạn cần nắm vững:
- Công Thức Đổi Cơ Số: \log_a b = \frac{\log_c b}{\log_c a}logab=logcalogcb Công thức này cho phép bạn đổi logarit từ cơ số (a) sang cơ số (c).
- Logarit của Tích: \log_a (bc) = \log_a b + \log_a cloga(bc)=logab+logac Logarit của một tích bằng tổng các logarit của các thừa số.
- Logarit của Thương: \log_a \left(\frac{b}{c}\right) = \log_a b – \log_a cloga(cb)=logab−logac Logarit của một thương bằng hiệu các logarit của tử số và mẫu số.
- Logarit của Lũy Thừa: \log_a (b^c) = c \log_a bloga(bc)=clogab Logarit của một lũy thừa bằng tích của số mũ và logarit của cơ số.
- Logarit của 1: \log_a 1 = 0loga1=0 Bất kỳ logarit nào của 1 đều bằng 0.
- Logarit của Chính Nó: \log_a a = 1logaa=1 Logarit của một số với chính nó làm cơ số luôn bằng .
3. Tính Chất Của Logarit
Logarit có một số tính chất quan trọng giúp đơn giản hóa các phép toán:
- Tính Chất Đơn Điệu: Hàm logarit là hàm đơn điệu tăng nếu cơ số (a > 1) và là hàm đơn điệu giảm nếu (0 < a < 1).
- Tính Chất Liên Tục: Hàm logarit là hàm liên tục trên khoảng ((0, +\infty)).
- Tính Chất Đạo Hàm: Đạo hàm của hàm logarit tự nhiên (\ln x) là (\frac{1}{x}).
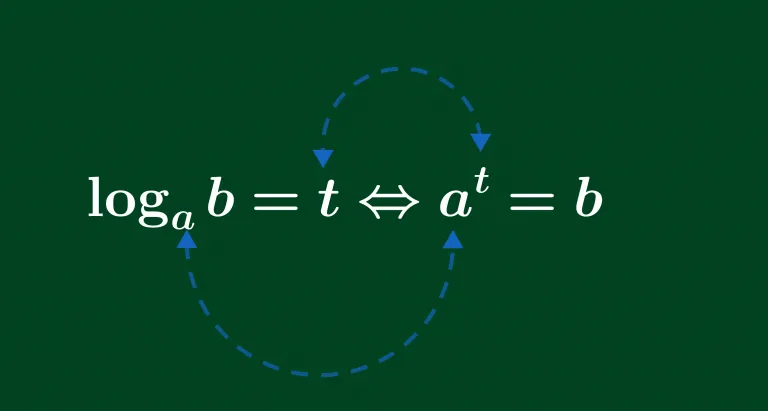
4. Ứng Dụng Của Logarit
Logarit có nhiều ứng dụng trong các lĩnh vực khác nhau như:
- Toán Học: Giải các phương trình mũ và logarit, tính toán trong giải tích.
- Khoa Học Máy Tính: Phân tích độ phức tạp của thuật toán, đặc biệt là trong các thuật toán tìm kiếm và sắp xếp.
- Kinh Tế Học: Mô hình hóa tăng trưởng kinh tế, lãi suất kép.
- Vật Lý: Tính toán trong các hiện tượng phân rã phóng xạ, sóng âm.
5. Ví Dụ Minh Họa
- Ví dụ 1: Tính (\log_2 32). Giải: (2^5 = 32) nên (\log_2 32 = 5).
- Ví dụ 2: Tính (\log_3 81). Giải: (3^4 = 81) nên (\log_3 81 = 4).
- Ví dụ 3: Tính (\log_5 125). Giải: (5^3 = 125) nên (\log_5 125 = 3).
6. Tài Liệu Tham Khảo
Để tìm hiểu thêm về các công thức logarit và cách áp dụng chúng, bạn có thể truy cập trang web giasutoanvan.com. Đây là một nguồn tài liệu hữu ích, cung cấp nhiều thông tin chi tiết và các bài viết về các khái niệm toán học và ứng dụng thực tiễn.

Kết Luận
Việc nắm vững các công thức logarit là rất quan trọng trong học tập và ứng dụng thực tiễn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Đừng quên truy cập giasutoanvan.com để cập nhật thêm nhiều thông tin và tài liệu học tập bổ ích.


